Understanding Copy-on-write Value Types in Swift
In Swift, the standard collection types like Array<Element> and String are implemented as structs and have value semantics. So when you
assign an array to a new variable or pass it as an argument to a function, a copy of the array is created. Of course instances of these
collection types can be very large and contain thousands or even millions of elements. Thus, it would not be very efficient to perform a deep
copy of all the elements every time an array or a string is passed as an argument to a function. Swift uses copy-on-write
to decide when a copy is really necessary in order to maintain value semantics.
The way this works is that each array instance internally has a reference that points to a buffer which contains the actual elements. When an array is assigned to a new variable, Swift will only perform a shallow copy at first. At this point both instances of the array share a reference to the same buffer. Once you start mutating one of the arrays (e.g., by appending or removing an element) Swift performs a deep copy and makes sure that both instances have a separate buffer.
This blog post shows how Swift’s copy-on-write mechanism works in detail by implementing a Stack<Element> value type. For the sake of simplicity, the type
has some serious limitations:
- Instances of
Stack<Element>have a fixed capacity Stack<Element>doesn’t conform to any of Swift’s collection protocolsStack<Element>doesn’t have a conditional conformance toEquatableorHashable
Thus, this code should not be used in production. If you ever want or need to create a stack type, you should probably just wrap
a regular Swift array (or use the Array<Element> directly).
That being said, let’s now have a look at how we can use the stack type.
Step 1: Creating an instance of Stack<Int>
import Stack
var stack1 = Stack<Int>(capacity: 5)
stack1.push(10)
stack1.push(20)
stack1.push(30)
print("stack1: ", stack1) // stack1: [10, 20, 30]
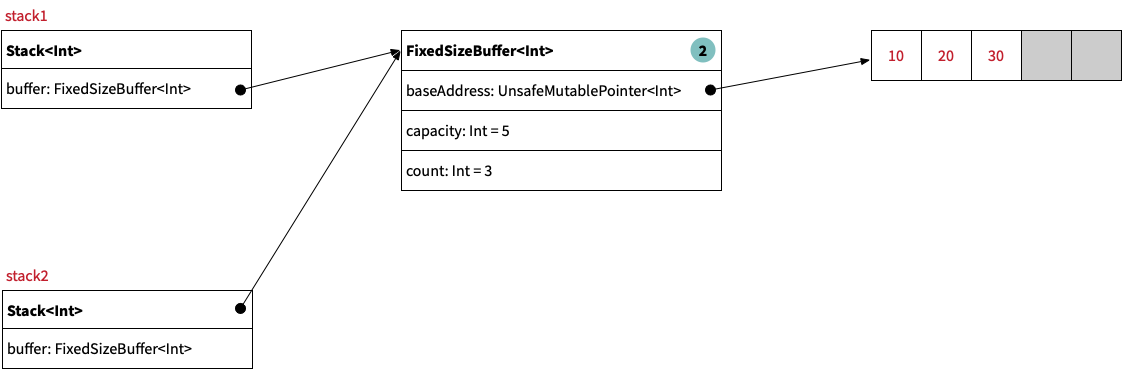
The following image shows what stack1 looks like in memory. It has a pointer to an instance of the FixedSizeBuffer<Int> class which
manages a raw buffer via an UnsafeMutablePointer<Int>. As you can see, the fixed-size buffer currently has a reference count of 1:

Step 2: Creating a copy of the stack instance
We can create a copy of stack1 by assigning it to a new variable:
var stack2 = stack1 // At this point, both stacks share the same buffer.
print("stack1: ", stack1) // stack1: [10, 20, 30]
print("stack2: ", stack2) // stack2: [10, 20, 30]
As shown in the following image, both stacks now reference the same fixed-size buffer which therefore has a reference count of 2:
Step 3: Mutating one of the copies
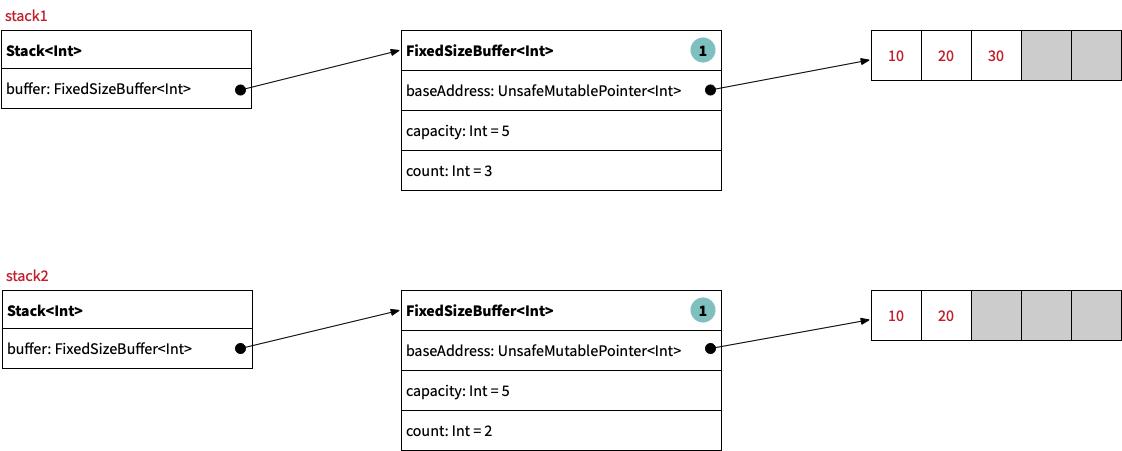
Finally, we pop an element from stack2:
stack2.pop() // To maintain value semantics, stack2 clones the
// shared buffer before performing the pop() operation.
print("stack1: ", stack1) // stack1: [10, 20, 30]
print("stack2: ", stack2) // stack2: [10, 20]
The Stack<Element> type recognized that we are mutating a stack instance which shares its internal buffer with another stack instance.
Therefore, in order to preserve value semantics, it creates a deep copy of the fixed-size buffer before performing the mutation:
Implementation
Let’s look at the implementation of the Stack<Element> type. The key section of this code is the computed property bufferForWriting.
Whenever we want to mutate the stack, we access its internal fixed-size buffer via this property. It uses the built-in function
isKnownUniquelyReferenced() to test whether there
is only one stack instance that references the buffer. If the buffer is shared with another stack, a new copy of the buffer is created:
public struct Stack<Element>: CustomStringConvertible {
var buffer: FixedSizeBuffer<Element>
public init(capacity: Int) {
self.buffer = FixedSizeBuffer(capacity: capacity)
}
var bufferForWriting: FixedSizeBuffer<Element> {
mutating get {
if !isKnownUniquelyReferenced(&buffer) {
buffer = FixedSizeBuffer(cloning: buffer)
}
return buffer
}
}
public var count: Int { buffer.count }
public var capacity: Int { buffer.capacity }
public var isEmpty: Bool { count == 0 }
public mutating func push(_ element: Element) {
precondition(count < capacity, "Can't push element onto a full stack")
bufferForWriting.append(element)
}
@discardableResult
public mutating func pop() -> Element {
precondition(!isEmpty, "Can't pop last element from an empty stack")
return bufferForWriting.removeLast()
}
public func peek() -> Element? {
guard !isEmpty else {
return nil
}
return buffer[count - 1]
}
public var description: String {
var result = "["
result += (0..<count)
.map { String(reflecting: buffer[$0]) }
.joined(separator: ", ")
result += "]"
return result
}
}
The FixedSizeBuffer<Element> class is not shown here, but you can find the full source code plus a few unit tests on GitHub at the following
URL: https://github.com/tonisuter/COW-Stack.